本文主要列出幾個(gè)已有的雙曲率曲面類型的典型例子丘侠，以便我們可以檢驗(yàn)這類非旋轉(zhuǎn)對(duì)稱曲面的基本概念徒欣。
變形系統(tǒng)系列（四）-雙曲面型及其曲面法通用理論
為了形成變形圖像打肝，我們需要成像系統(tǒng)內(nèi)具有雙曲率的折射(或反射)表面脂新。此外，我們需要雙曲率曲面如此對(duì)齊粗梭，來(lái)保證曲面的對(duì)稱平面與x-z和y-z平面重合争便。這保證了我們的光學(xué)系統(tǒng)將具有雙平面對(duì)稱性，因此我們可以在x-z和y-z對(duì)稱平面上實(shí)現(xiàn)不同的放大倍數(shù)断医。將選擇光軸作為對(duì)稱平面的交點(diǎn)線滞乙。
現(xiàn)在讓我們列出幾個(gè)已有的雙曲率曲面類型的例子，以便我們可以檢驗(yàn)這類非旋轉(zhuǎn)對(duì)稱曲面的基本概念鉴嗤。
從數(shù)學(xué)的角度來(lái)看斩启，比較簡(jiǎn)單的雙曲率曲面類型可能是一個(gè)橢圓拋物面，其表面矢高z在笛卡爾坐標(biāo)下表示為
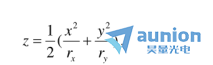
其中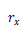
和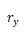
分別是x-z和y-z對(duì)稱平面曲率的主半徑醉锅。平行于x-y平面的截面是橢圓兔簇，垂直于x-y平面的截面是拋物線。
從加工的角度來(lái)看荣挨，比較簡(jiǎn)單的雙曲率曲面類型可能是環(huán)形曲面男韧，表示為
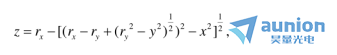
同樣朴摊，其中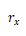
和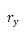
是對(duì)稱平面曲率的主半徑默垄。環(huán)面的四階近似矢高為
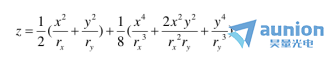
注意，當(dāng)前變形系統(tǒng)設(shè)計(jì)中使用較廣泛的雙曲率曲面類型是圓柱面甚纲，這是環(huán)面的一種特殊情況口锭，其中一個(gè)主曲率半徑等于無(wú)窮大。四階近似下圓柱面的表面矢高方程為
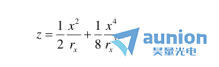
或者,
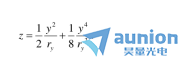
取決于主半徑等于無(wú)窮大介杆。
從光學(xué)測(cè)試的角度來(lái)看鹃操，比較簡(jiǎn)單的雙曲率曲面類型可能是橢球面，表達(dá)式為
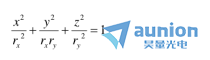
該曲面的矢高方程表示為扁截面春哨，四階近似為
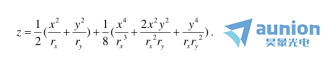
從上面已有的雙曲率曲面類型的例子中荆隘，我們可以看到，對(duì)于這類曲面赴背，表面垂度方程一般可以寫(xiě)成四階近似的形式
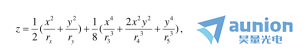
在這里椰拒，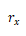
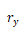是兩個(gè)主截面表面的曲率半徑，
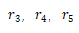是具有長(zhǎng)度尺寸的一定系數(shù)凰荚。注意燃观，在這個(gè)方程中，我們?cè)试S
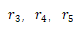在四階非球面這兩個(gè)主要部分不同于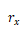
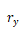便瑟。
我們應(yīng)該注意到缆毁，當(dāng)主要部分是圓的形式(例如一個(gè)環(huán)面)，我們有
和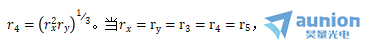
我們回到球面的特殊情況到涂。因此脊框，由上式我們通過(guò)適當(dāng)選擇
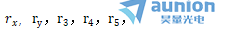可以得到雙曲率曲面類型的矢高方程颁督，直到四階近似。
現(xiàn)在浇雹，在完成了一般的雙曲率曲面矢高方程之后适篙，為了應(yīng)用一般的射線折射方程，有必要得到入射點(diǎn)表面法線方向余弦的方便表達(dá)式箫爷。
我們把曲面方程寫(xiě)成
那么對(duì)于相鄰點(diǎn)
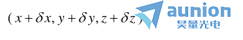它也在這個(gè)曲面上嚷节，我們會(huì)得到
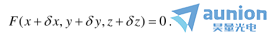
由泰勒展開(kāi)，可將上式改寫(xiě)為
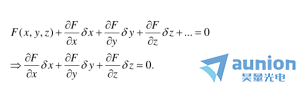
從這個(gè)方程中我們可以看出虎锚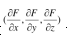，向量
垂直于向量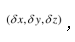
由于后者被限制在曲面上硫痰，所以向量
定是沿曲面法線在點(diǎn)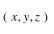
處的向量。
因此窜护，曲面法線的方向余弦為
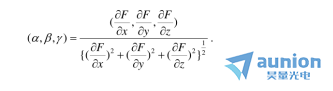
相關(guān)文獻(xiàn)：
《幾何光學(xué) 像差 光學(xué)設(shè)計(jì)》（第三版）——李曉彤 岑兆豐
更多詳情請(qǐng)聯(lián)系昊量光電/歡迎直接聯(lián)系昊量光電
關(guān)于昊量光電：
上海昊量光電設(shè)備有限公司是光電產(chǎn)品專業(yè)代理商效斑，產(chǎn)品包括各類激光器、光電調(diào)制器柱徙、光學(xué)測(cè)量設(shè)備缓屠、光學(xué)元件等，涉及應(yīng)用涵蓋了材料加工护侮、光通訊敌完、生物醫(yī)療、科學(xué)研究羊初、國(guó)防滨溉、量子光學(xué)、生物顯微长赞、物聯(lián)傳感晦攒、激光制造等；可為客戶提供完整的設(shè)備安裝得哆，培訓(xùn)脯颜，硬件開(kāi)發(fā)，軟件開(kāi)發(fā)贩据，系統(tǒng)集成等服務(wù)栋操。
您可以通過(guò)我們昊量光電的官方網(wǎng)站www.wjjzl.com了解更多的產(chǎn)品信息，或直接來(lái)電咨詢4006-888-532乐设。
展示全部 
展示全部
