穩(wěn)定腔激光器發(fā)出的激光束是一種具有特殊結(jié)構(gòu)的高單色性的高斯光束尊剔，它具有最小橫向發(fā)散角，在光學(xué)元件邊緣的衍射損耗最小。此外须误，高斯光束通過自由空間的傳播和通過無像差透鏡的變換時(shí)挨稿，除輪廓比例因子外，將始終保持高斯型分布京痢。我們將首先介紹高斯光束的性質(zhì)奶甘，然后討論激光通過薄透鏡后的性質(zhì)變化，最后介紹激光擴(kuò)束鏡祭椰。
高斯光束及通過薄透鏡時(shí)的變換及激光擴(kuò)束鏡（一）
高斯光束的基本性質(zhì)
穩(wěn)定腔激光器發(fā)出的激光束是一種具有特殊結(jié)構(gòu)的高單色性的高斯光束方淤，它具有最小橫向發(fā)散角钉赁，在光學(xué)元件邊緣的衍射損耗最小。此外携茂，高斯光束通過自由空間的傳播和通過無像差透鏡的變換時(shí)你踩，除輪廓比例因子外，將始終保持高斯型分布讳苦。
電矢量沿z軸方向傳播的高斯光束的性質(zhì)可以由下面三個(gè)方程式來決定：
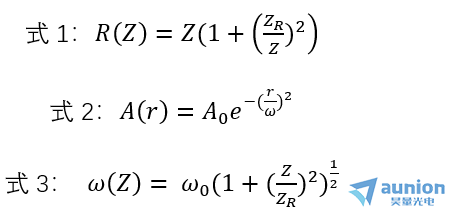
上式中带膜，R(Z)是距離坐標(biāo)原點(diǎn)（束腰）Z處的高斯光束的波陣面的曲率半徑（為球面），A(r)是高斯光束電矢量在r方向（也就是垂直于光波傳播方向）的振幅鸳谜，A0是波陣面中心的振幅膝藕，ω為光束的光斑半徑，其中
分析式1可以知道咐扭，當(dāng)Z 趨于0的時(shí)候芭挽，R(Z)趨于無窮，即此時(shí)波陣面為平面蝗肪；當(dāng)0≤|Z|≤ZR的時(shí)候袜爪，R(Z)逐漸減小，并且R(Z)>Z穗慕，即波陣面的曲率中心不在原點(diǎn)并且會(huì)隨Z變化而變化，如下圖所示妻导。當(dāng)Z= ±ZR時(shí)逛绵，ZR取到極小值±2ZR；而當(dāng)Z ?±ZR時(shí)倔韭，R(Z)重新增大术浪，當(dāng)Z趨于無窮的時(shí)候，變成平面波寿酌。
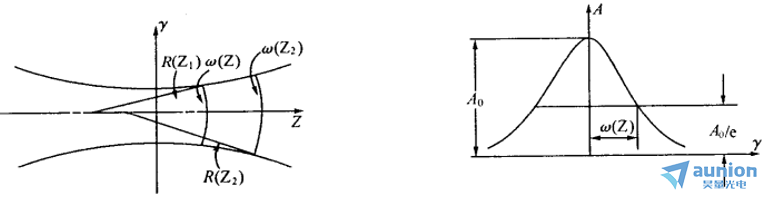
分析式2可以知道胰苏，高斯光束電矢量的振幅隨高斯函數(shù)變化，在光束中心（r = 0）的地方振幅最大醇疼，如上圖所示硕并，所以高斯光束的光斑沒有清晰的輪廓法焰。式3中的光斑半徑是振幅為A0/e，它又是Z的函數(shù)倔毙，如上圖所示，當(dāng)Z = 0 的時(shí)候，ω(0)= ω0為最小毁嗦，它是高斯光束的束腰瓜挽，ω0稱為腰粗，Z ?ZR的時(shí)候么库，有
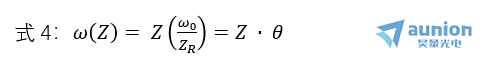
上式中傻丝，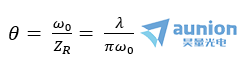
是高斯光束的遠(yuǎn)場(chǎng)發(fā)散角，用來描述高斯光束的發(fā)散角诉儒。2ZR為高斯光束的準(zhǔn)直區(qū)葡缰，在這個(gè)范圍內(nèi)，高斯光束的光斑半徑變化緩慢允睹，準(zhǔn)直性較好运准。在準(zhǔn)直區(qū)的兩端，Z= ZR缭受，有ω= √2 ω0胁澳，光斑半徑僅為束腰半徑的√2倍。當(dāng)Z ?±ZR米者，為高斯光束的遠(yuǎn)場(chǎng)區(qū)韭畸，與普通球面波的變化規(guī)律完全相同。所以蔓搞，普通球面波可以看作束腰半徑ω_0=0的高斯光束胰丁。
所以，對(duì)于一個(gè)確定波長(zhǎng)的高斯光束喂分，當(dāng)ω0一定的時(shí)候锦庸，R(Z)、ω(Z)蒲祈、θ(Z)都可以確定甘萧，所以腰粗ω0是高斯光束的一個(gè)主要特征參量。
由于光束參數(shù)R(Z)梆掸、ω(Z)完全確定了高斯光束的幾何形狀扬卷，為了討論方便，引入復(fù)曲率半徑q(Z)酸钦，即
當(dāng)Z = 0時(shí)怪得，R(0)→∞，于是
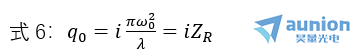
將式1、式3和式6代入式5得到
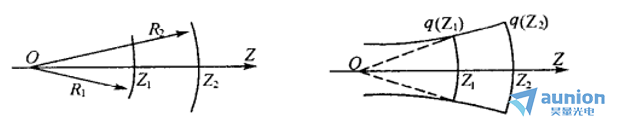
由此可見徒恋，q在高斯光束傳播中的作用與球面波的曲率半徑在球面波的傳播中的作用一樣蚕断，如上圖所示，這表明因谎，激光束是電磁波中光波段的一種新的傳播形式基括，它的傳播具有普遍的規(guī)律性，可以將普通球面波的傳播規(guī)律認(rèn)為是激光束的一種特殊情況财岔。
相關(guān)文獻(xiàn)：《幾何光學(xué) 像差 光學(xué)設(shè)計(jì)》（第三版）——李曉彤 岑兆豐
您可以通過我們昊量光電的官方網(wǎng)站www.wjjzl.com了解更多的產(chǎn)品信息风皿，或直接來電咨詢4006-888-532，我們將竭誠為您服務(wù)匠璧。
展示全部 
展示全部
