什么是快速傅里葉變換怕享？
快速傅里葉變換
模擬信號(hào)使用傅里葉變化公式念链，數(shù)字信號(hào)可以采用離散傅里葉變化公式盼忌，但是離散傅里葉變化公式計(jì)算量大，所以對(duì)于離散的信號(hào)掂墓，現(xiàn)
在都是采用快速傅里葉變化（Fast Fourier Transformation)
這里以一個(gè)隨機(jī)信號(hào)表示離散的信號(hào)
依據(jù)上述公式谦纱，如果計(jì)算X(k)，乘法計(jì)算8（num）次君编，加法計(jì)算7（num-1）次跨嘉，計(jì)算所有的頻譜，需要乘法64（num^2）次吃嘿，加
法計(jì)算56（num×(num-1)）次祠乃。假設(shè)乘法使用四個(gè)時(shí)間周期T，加法使用一個(gè)時(shí)間周期T兑燥，那么8個(gè)數(shù)據(jù)占據(jù)的周期大約是312T
將這個(gè)公式和一些軟件計(jì)算的結(jié)果進(jìn)行對(duì)比亮瓷，結(jié)果是一樣的
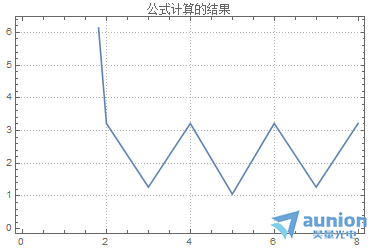
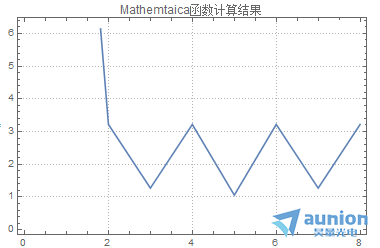
FFT
下述公式，首先將系數(shù)奇數(shù)項(xiàng)和偶數(shù)項(xiàng)分開(kāi)降瞳，然后偶數(shù)想提出公因式e^(-I 2π/N k)嘱支，保持兩個(gè)多項(xiàng)式的e指數(shù)有相同的形式蚓胸，最后合并
2和N，奇數(shù)和偶數(shù)項(xiàng)構(gòu)成新的多項(xiàng)式除师。
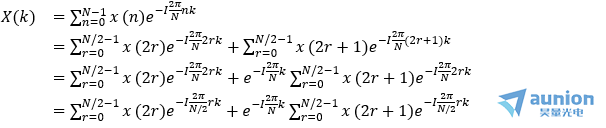
假設(shè)序列的長(zhǎng)度為8沛膳，按照上述規(guī)則，將序列按照奇偶不斷的分裂汛聚，直到最后
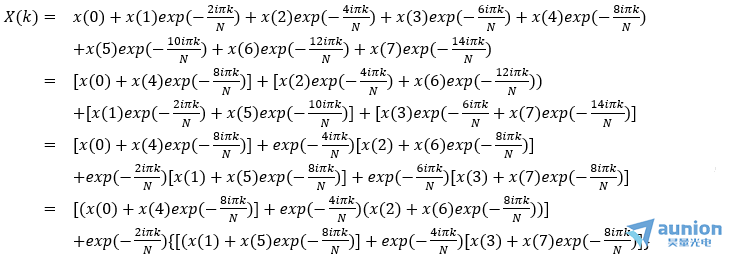
觀察最后一個(gè)等號(hào)后的公式锹安，從小括號(hào)，到中括號(hào)倚舀，到大括號(hào)八毯，每個(gè)括號(hào)作為一層，可以得到網(wǎng)上的蜘蛛圖
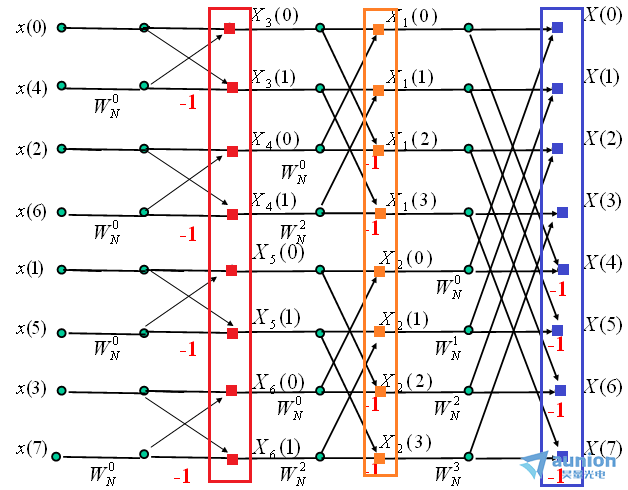
首先從小括號(hào)看起瞄桨，小括號(hào)內(nèi)x0,x2,x4,x6沒(méi)有系數(shù)话速，而x1,x3,x5,x7的系數(shù)是exp(-8iπk/N)，k從0到7內(nèi)取任何整數(shù)芯侥，exp(-8iπk/N)無(wú)
非是+1或者是-1泊交，所以看到在x1,x3,x5,x7后面可能跟隨著兩個(gè)系數(shù)W_N^0或者-1，就是表示相乘的意思柱查，然后在紅色方框內(nèi)相遇
廓俭，相遇代表相加。他們是第一層唉工，同時(shí)作為下一層的輸入研乒。下一層輸入的系數(shù)是exp(-8iπk/N)，k從0到7改變淋硝，系數(shù)可出現(xiàn)四種雹熬，
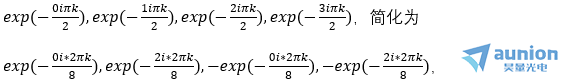
按照?qǐng)D上的表示應(yīng)該是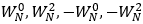
，同時(shí)它也作為第二層結(jié)果谣膳，同理可以得到第三層結(jié)構(gòu)竿报。每一層結(jié)構(gòu)有8個(gè)數(shù)據(jù)，每個(gè)數(shù)據(jù)
都結(jié)構(gòu)都是做了一次乘法和一次加減法继谚。相對(duì)于DFT而言烈菌，DFT做乘法64次，而這里做的乘法只有不到8*lg8花履，也就是大約24次左右
芽世，因此能夠節(jié)省很多時(shí)間。
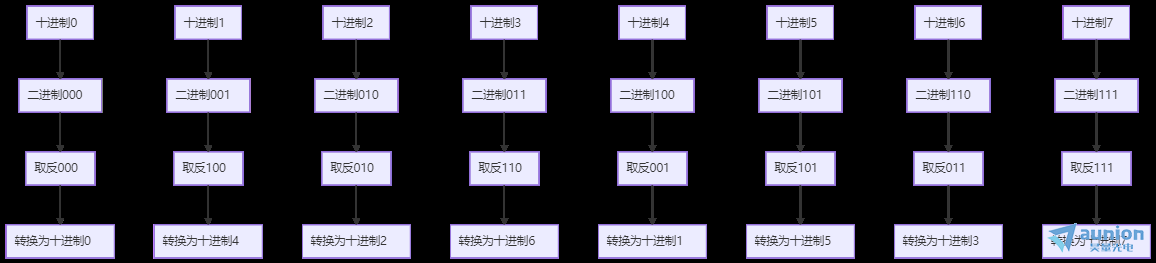
上面的叉形圖中诡壁，最后的數(shù)字排列也是存在規(guī)律的济瓢。
二維傅里葉變化FFT2是對(duì)一個(gè)二維矩陣，先做一次FFT欢峰，然后轉(zhuǎn)置后再做一次FFT葬荷。這里以一個(gè)實(shí)際的例子作為參考涨共，輸入的信號(hào)是一個(gè)3*3的矩陣
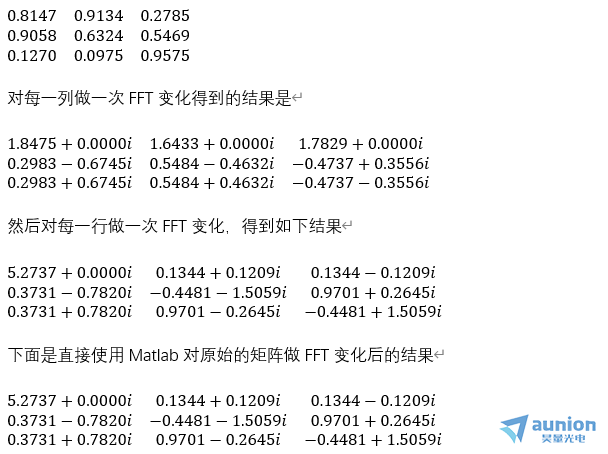
如果用matlab表示信號(hào)x，兩次FFT變化可以寫為fft(fft(x),3,2)宠漩，一次FFT變化可以記作fft2(x)
您可以通過(guò)我們的官方網(wǎng)站了解更多的產(chǎn)品信息举反，或直接來(lái)電咨詢4006-888-532。
展示全部 
展示全部
